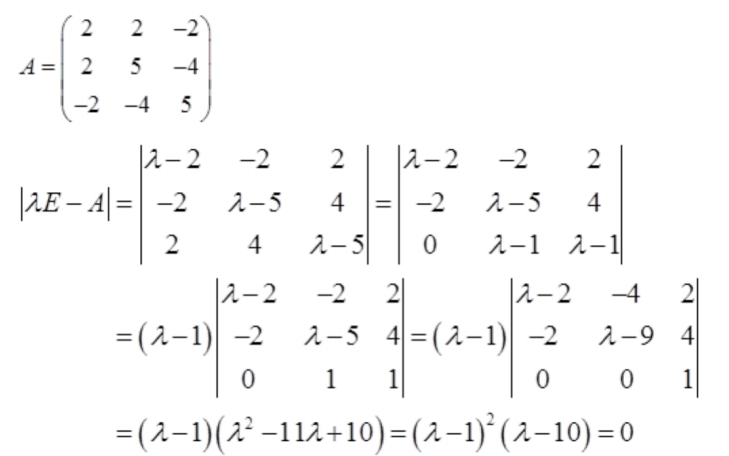你可能感兴趣的试题

• 用正交变换将二次型f（x₁，x₂，x₃）＝2x₁₂＋3x₂₂＋3x₃₂＋4x₂x₃化为标准形为（）。
  查看试题
• 已知二次型f（x₁，x₂，x₃）＝5x₁₂＋5x₂₂＋dx₃₂－2x₁x₂＋6x₁x₃－6x₂x₃的秩为2。则d为（）。
  查看试题
• 设矩阵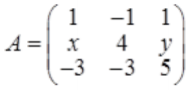，已知A有三个线性无关的特征向量，λ＝2是A的二重特征值，则可逆矩阵P为（），使P－1AP为对角矩阵。
  查看试题
• 已知矩阵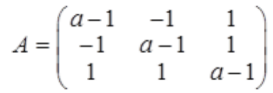，且A－E为降秩矩阵。当A的特征值之和最小时，求出正交矩阵P为（），使PTAP为对角矩阵。
  查看试题
• 设矩阵可逆，向量＝（1，b，1）T是矩阵A*的一个特征向量，λ是α对应的特征值，其中A*是矩阵A的伴随矩阵，则非零实数a、b、λ为（）。
  查看试题
• 设n阶矩阵A＝（a_ij），其中，则A的特征值为（）。
  查看试题